¿Utilizas medias aritméticas para el cálculo de métricas? ¡Cuidado!

Algo que aprendemos bastante temprano, desde el colegio, son las nociones básicas sobre Estadística. Asimilamos en qué consiste trabajar con una muestra de datos más o menos grande y aprendemos a calcular la media aritmética y algunos otros conceptos como la mediana, la varianza, etcétera. Entonces, ¿por qué nos conformamos solo con la media? De hecho, es posible que ahora mismo estés yendo a Google para recordar cuáles eran esos otros conceptos que he nombrado.

Así que me atrevo a decir que la media aritmética vuela en primera clase, pero el resto se quedan en tierra. Llevo años observando este comportamiento en muchas organizaciones, yo mismo he caído en el error más de una vez. Cuando acabes de leer este post, espero que pienses “una y no más, Santo Tomás”.

Un par de ejemplos para entender el problema

Esta vez no voy a poner el clásico ejemplo que usamos muchos agilistas de salir a correr varios días y calcular la media. Vamos a algo más real e impactante: soy un trabajador cuyos ingresos son variables en función de la época. A lo largo de un año, en los meses impares me queda un salario neto de 1000€, mientras que en los pares la cifra asciende a 4000€. La media aritmética sale exactamente 2500€ al mes, así que me aventuro a firmar una hipoteca con una letra de 1500€ mensuales. ¿Hace falta que explique qué va a pasar con mi casa? Creo que ya lo hemos visto en los telediarios.

El banco me ha embargado porque solo presté atención a mi sueldo medio, sin tener en cuenta la dispersión de los valores con respecto a la media. De ninguna manera puedo garantizar que el valor medio se vaya a cumplir siempre. Es lo que tienen los promedios, que nos sirven para obtener conclusiones muy generales, pero nunca determinantes o vinculantes.

Si el salario y la vivienda nos preocupan, la integridad física aún más. Vamos a ver otro ejemplo: sufro un incendio en mi casa, llamo a emergencias y casi al instante aparece el camión de bomberos con esa verbena de sirenas y luces. Quien hizo los cuadrantes de turnos tuvo la idea de combinar bomberos veteranos con jóvenes para que estos últimos aprendan de la experiencia de los primeros. De los ocho profesionales que se subirán al camión, tres de ellos son recién titulados y tienen 20 años, mientras que los otros cinco están cercanos a la jubilación, tienen 59 años. La media de edad sale en 44 años aproximadamente, es decir, una edad óptima para estar en plenitud y rescatar a alguien de las llamas.

¿Cómo termina la historia? No lo sé, pero sí que sé que la persona que diseñó el cuadrante de turnos no tuvo en cuenta que la edad que más se repite es la de 59 años y que me atendería uno de los veteranos con una probabilidad del 62,5%. Habrá personas con esa edad capaces de mover vigas, cargar con mi peso o soportar altas temperaturas, pero ya entendéis por dónde voy.

¿Cómo nos ayuda la Estadística a tener una visión más realista?

Una visión más realista y, sobre todo, ¡más sensata! Quizá estés pensando que los ejemplos anteriores son bastante obvios y saltan a la vista, no te quito razón. Cuando la muestra de datos es muy pequeña, todo se ve muy claro, pero ¿qué pasa cuando hablamos de miles y miles de datos? Yéndonos al mundo del software, si calculamos una media aritmética en base a las tareas resueltas por un equipo durante los tres últimos años, probablemente la muestra es tan grande que quizá los árboles te impidan ver el bosque.

En el ejemplo del autónomo y su salario no tuvimos en cuenta esa dispersión de valores con respecto a la media. Antes de utilizar la media aritmética para fines importantes, debemos asegurarnos de que esa dispersión es baja y no alta. Cuando es baja significa que la media sí es representativa de los valores de la muestra porque no hay mucha distancia entre ella y dichos valores. Para ello, debemos apoyarnos en la varianza y la desviación típica, que finalmente nos darán un coeficiente de variación. No vamos a entrar en cómo calcularlas, ya que nos extenderíamos demasiado.

En el ejemplo de los bomberos, además de tener una dispersión alta, no tuvimos en cuenta el valor que más se repetía dentro de la media, es decir, la moda, que nos permite establecer probabilidades de ocurrencia.

Lean y la Estadística en el desarrollo de software

A estas alturas y con ese par de ejemplos, creo que ya tenemos claro que calcular la media no es suficiente. También lo tuvo claro la compañía Toyota cuando en 1955 concibió su Toyota Production System (TPS), lo que supuso el embrión de Lean y, a su vez, de Kanban.

Pero empecemos por el principio: Lean tiene como objetivo aumentar el valor que entregamos al cliente, poniendo el foco en dos aspectos principales:

1. La eficiencia de los procesos eliminando desperdicios (también llamados Muda) y, por ende, mejorando los tiempos de entrega.
2. La mejora continua en pequeños pasos, también llamada Kaizen.

Para ambos aspectos necesitamos métricas, ya que de otra manera estaríamos basándonos en sensaciones y opiniones subjetivas. Para ello, Lean considera el tiempo como la unidad clave sobre la que poner foco y nos ofrece dos métricas de tiempo tremendamente importantes:

• Lead Time (LT) o el tiempo transcurrido desde que aceptamos una tarea demandada por un cliente hasta que entregamos dicha tarea.
• Cycle Time (CT) o el tiempo transcurrido desde que empezamos a procesar una tarea hasta que la completamos.

Estas métricas se pueden calcular con medias aritméticas, pero como vimos antes, corremos el riesgo de tener una visión demasiado general y perdernos el detalle. Vamos a indagar en la predictibilidad de Lean y después pasaremos a ver cómo utilizar estas métricas con mejor puntería.

Dejar a un lado las estimaciones y pasar a ser predictibles

Algo en lo que insiste Lean es en que nuestros procesos sean predictibles, es decir, que podamos conocer con seguridad cómo se va a comportar nuestro sistema o flujo para poder dar respuesta a la demanda de una manera fiable. En definitiva, nos permite afirmar que “sabemos que tardamos 3 días de media en entregar una tarea” porque nos lo dice el Lead Time, nos estamos basando en experiencias pasadas con datos concretos.

Si la predictibilidad es el vino de calidad a la temperatura óptima, las estimaciones son el garrafón de marca blanca. Hicieron su función, estaban ahí cuando empezamos a trabajar el delivery, pero tienen muchos inconvenientes y es normal que con el tiempo queramos hilar más fino. Al fin y al cabo suponen una técnica no orientada a datos, se basan en sensaciones, creencias y especulaciones, poco más que un brindis al sol. En la mayoría de los casos tendremos grandes desviaciones con respecto a lo estimado. Al fin y al cabo, está demostrado que el ser humano es bueno analizando datos y actuando en consecuencia, pero no jugando a ser vidente.

Una vez aterrizada la predictibilidad, es crucial entender qué dos factores impactan negativamente en ella:

1. La variabilidad (también llamada Mura), que viene dada por procesos pobres o con falta de estandarización. Se me viene a la cabeza un ejemplo sobre algunas compañías telefónicas, esa sensación de llamar para que me resuelvan una incidencia y “a ver qué aventura me toca vivir hoy”. Nunca se resuelve (si es que llega a resolverse) de la misma manera, da la sensación de aleatoriedad: unas veces abren un ticket, otras me pasan con la persona responsable y otras se corta la llamada misteriosamente.
2. La sobrecarga (también llamada Muri), que viene dada por una falta de flexibilidad y versatilidad en el proceso o las personas involucradas. Pongo como ejemplo cuando una persona es la única especializada en algo concreto dentro del equipo y nos genera un cuello de botella cuando no está disponible. No podemos satisfacer la demanda en los tiempos deseados porque nadie más puede desempeñar esa función.

Tanto Mura como Muri son conocidos por matar la eficiencia y la predictibilidad de las organizaciones, así que debemos trabajar en esta dirección si queremos que nuestras métricas de tiempos no fluctúen. Venga, pasemos al plato principal.

Alternativas a la media aritmética

O más bien, cómo hacer que esa media sea más fiable y aproximada a la realidad. Para ello, Kanban acude al rescate y nos echa una mano con sus Service Level Expectations.

Service Level Expectation (SLE) consiste en combinar una métrica de tiempo (por ejemplo, Lead Time) con una probabilidad de ocurrencia o suceso y se expresa de la siguiente manera: “tardamos en procesar una tarea 5 días o menos con una probabilidad del 85%” o “6,5 días o menos con una probabilidad de 95%”. Este pronóstico tiene su base estadística en los percentiles, que ordenan la muestra de datos de menor a mayor y calculan dónde está el límite con respecto al porcentaje especificado. Ese porcentaje, al fin y al cabo, es un margen de seguridad que nosotros fijamos en función de las necesidades. Los más utilizados en Kanban son p99, p95, p90 y p85, siendo este último el más popular por tener un buen equilibrio entre el riesgo asumido y el valor más cercano a la media aritmética. Sin embargo, te invito a que decidas tú mismo el percentil que consideres más oportuno en función del nivel de riesgo y compromiso que estés dispuesto a aceptar.

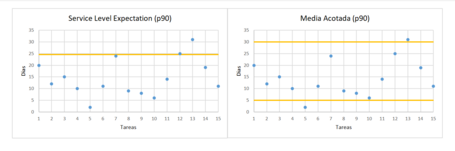
También podemos acudir a la media acotada, que consiste en calcular la media después de haber eliminado los valores del extremo inferior y superior. De esta manera, si acotamos al 80%, habremos eliminado el 10% de los valores inferiores y el 10% de los superiores. El objetivo es eliminar los casos más extremos y quedarnos con lo que consideramos es la muestra de datos más representativa de la realidad. Mientras que con SLE la media aumenta a medida que aumentamos el percentil (solo eliminamos el extremo superior), con la media acotada el resultado es más impredecible porque los valores que eliminamos de un extremo pueden compensar el del otro.

Por último, hablemos de cómo elegir ese porcentaje que necesitamos. No hay una norma general a seguir, basta con que apliques el sentido común y analices el contexto en el que te mueves. Poniendo como ejemplo la consultoría en el desarrollo de Software, si hemos establecido una relación de confianza mutua entre cliente y proveedor, probablemente utilice un SLE con p85 para transmitirle con cierta seguridad unos tiempos de entrega razonables. Sin embargo, ante un cliente más difícil de llevar y con poca tolerancia a las desviaciones, utilice un p95 o p99 para no pillarme los dedos.

Hasta aquí, la lectura de hoy, hemos empezado hablando de estadística básica con algunos ejemplos sencillos para después entrar de lleno en Lean, Kanban y su predictibilidad. Al fin y al cabo, todo está relacionado, ya que, sin darnos cuenta, las medias aritméticas están presentes en la mayoría de las facetas de nuestra vida y en lo que nos rodea. Calcular solo la media es muy sencillo, basta con coger una calculadora o aplicar una fórmula en una hoja de cálculo, pero quiero que seas consciente de sus limitaciones. También quiero destacar que cuando hablamos de predictibilidad, acuerdos o expectativas, independientemente de cómo generemos los datos, es importante tener en cuenta la probabilidad de estar por encima o por debajo de dicho dato. Nada más, ¡espero haberte convencido!