Estadísticas bayesianas y estadísticas frecuentistas: así ayudan a tu negocio.

Nunca me hubiera parado a investigar qué es eso de las estadísticas bayesianas (por mí, como si hay cuarenta tipos de estadísticas...) si no hubiera sido por la ponencia de Zalando que se presentará en el #BDS15 el próximo 15 de octubre. Acudiendo a la fuente, en el tech blog Zalando, "Vestimos Código" de este servicio de moda con entrega a domicilio, se daban las pistas básicas.

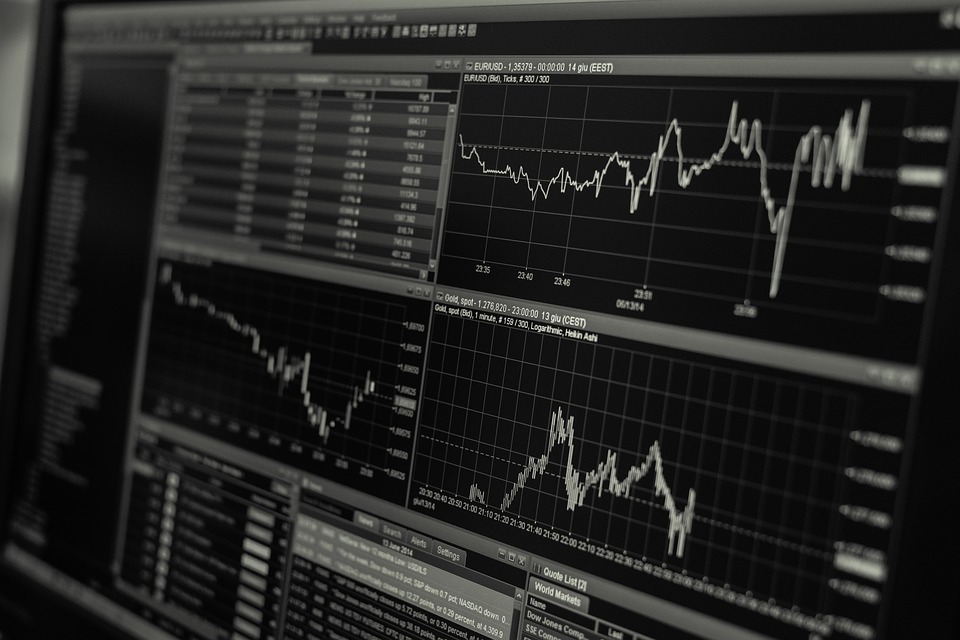
Se mandan muchos envíos al día pero hay que saber el peso de cada uno para comprobar que la facturación de la paquetería por DHL es la correcta. Pesar cada paquete es una trabajo adicional al de preparar cada envío. En la mayoría de los casos, encima es un paso redundante.

Se pensó que ya había información previa (y gratuita) de lo que pesaban las prendas, y que en la mayoría de los casos se podía sacar una estimación solo con el tamaño de la caja empleada y el número de artículos incluidos.

Pensado todo ello, sólo faltaba encontrar el umbral de confianza, para preparar el escenario sobre el que tomar las decisiones. Los técnicos primero tuvieron la intuición, y luego vieron en los modelos bayesianos la fundamentación matemática suficiente para dar respaldo al proyecto.

Los resultados fueron inmediatos: los operarios pudieron centrarse en hacer su trabajo más rápido (preparar los envíos); los cálculos de los pesos apenas se desviaron, de hecho se hicieron más fiables que el anterior sistema de pesado manual paquete a paquete en la báscula; se pudo reforzar el concepto de negocio de Zalando: "el probador en casa".

Y es que no importa el número de devoluciones que tenga cada pedido, porque precisamente se trata de eso, de que la gente use el servicio primero teniendo la confianza de que si no le vale o no le guste lo devuelva sin compromiso, y con esa garantía asegurada y demostrada, vuelva a comprar cuando quiera y cuantas más veces mejor.

Se trata de ir captando a las mejores compradoras y más asiduas de la Red, a la larga cualquier devolución que se produzca compensa si se tiene bien calculado su coste y la proporción de devoluciones para diluir su coste entre el resto de gastos.

"A todo el mundo le gusta ahorrar dinero -y cuando se está ejecutando un gran negocio como Zalando, ahorrar dinero en cada pequeño detalle al hacer sus sistemas más eficientes puede significar el ahorro de millones de euros", señala Roland Vollgraf, del departamento de Inteligencia de Datos. Vamos a ver si nos podemos situar en una posición de entender algo sin ponernos matrices, integrales y derivadas.

Cómo funcionan las estadísticas bayesianas

Aquí un poco de teoría (y de historia). En general, las estadísticas bayesianas están consideradas como un subconjunto en la ciencia estadística. Tuvieron su momento de gloria cuando Thomas Bayes a mediados del 1700 formula su concepto de probabilidad inversa.

Cincuenta años antes había nacido la estadística de la mano de Chevalier de Maré cuando le preguntó a Blas Pascal (que acababa de diseñar la ruleta francesa de los casinos) acerca de cómo asegurarse apuestas en un juego de cartas a medida que se repartían, y éste acudió nada menos que a Pierre de Fermat (el del teorema del millón de dólares) para discutir el asunto.

Sin pretenderlo, habían creado una poderosa herramienta para organizar, interpretar y utilizar información con el fin de tomar mejores decisiones. Volver a agitar los dados en un cubilete nunca volvió a ser igual.

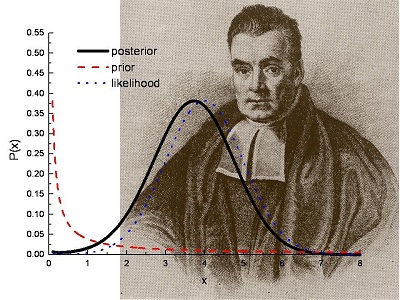
Llegó la teoría de los grandes números y Bayes argumenta su visión de la probabilidad introduciendo el concepto de la subjetividad o cómo cambian los juicios de una persona acerca de la ocurrencia de un evento a la luz de nueva información (evidencias) adicionales, y así prevaleció durante todo el s. XVIII gracias en especial al impulso dado por Laplace al análisis de datos.

Sin embargo, la ciencia matemática evolucionó por otros derroteros más empíricos basados en la instrumentación de las mediciones donde la intuición y la subjetividad no tenían cabida, desembocándose en la interpretación frecuentista de la probabilidad.

Karl Pearson y Francis Galton con "la regresión a la media" (que explicaría cosas como la sabiduría de las multitudes ahora tan evidentes en los comportamientos en Internet o por qué mucha gente toma decisiones con la expectativa de que “las cosas volverán a la normalidad”), y más tarde Ronald Fisher y otros sientan las bases del enfoque "objetivo" (depende exclusivamente del resultado de la prueba y no requiere ninguna referencia externa).

Este nuevo enfoque, basado en la noción de verosimilitud y en la interpretación frecuentista de la probabilidad, resultó ser relativamente fácil de aplicar en la práctica, lo que motivó su desarrollo imparable durante todo el s. XX, acentuándose con la aparición de software especializado para llevar a cabo los procesos de cómputo más comunes.

Sin embargo, algo fallaba. Y era eso de que "las estadísticas no mienten, sin embargo algunos estadísticos sí suelen". Si tenemos un pollo asado y dos personas, tocan a medio pollo cada una; pero eso no quiere decir que una se haya quedado con hambre y la otra saciada; ni siquiera que hayan tocado a la mitad cada una, quizás una tenía el pollo entero en su plato y la otra solo miraba.

Si hablamos de probabilidad de tener un cáncer o contagiarnos del VIH, de poco nos sirven las estadísticas generales poblacionales, queremos una a medida que se ajuste a nuestros parámetros genéticos y hábitos de vida.

Big Data Analytics en escena

Y es así como está volviendo a estar de moda los planteamientos bayesianos. Incluso algunos gurús de las matemáticas han advertido que, a partir del 2021, toda la estadística será bayesiana. ¿Por qué? Porque nuestro amigo el Big Data Analytics lo hace posible.

La estadística bayesiana se ha demostrado más eficaz para tratar ciertos asuntos de econometría y ciencias sociales en donde entran parámetros menos científicos como la filosofía, los sentimientos y el análisis de los comportamientos.

Antes, para que una estadística clásica o frecuentista tuviera validez, por ejemplo el reparto del share por parte de las cadenas de televisión, requería acudir al mínimo universo lo más representativo posible (cuestión de dinero, no se puede poner un medidor de Sofres en cada televisor).

Eso de entrada ya es trampa, porque los resultados de audiencia obtenidos van a depender de lo bien hecho que esté el muestreo, o de lo mucho que te quieras gastar preguntando a más gente (a toda la gente en un ideal imposible).

Para un bayesiano no hay tal problema, pues no depende del tamaño muestral, aunque obviamente una muestra más grande nos permitirá valorar mejor la adecuación de las conclusiones a la realidad.

Otra crítica a los frecuentistas es que sus pruebas de hipótesis solo sirven para afirmar (o refutar) una o su contraria, en lugar de poner el acento en la credibilidad de la hipótesis y su correlación con la realidad empírica analizada, cosa que sí hacen los bayesianos, que no están obligados a escoger "entre papá o mamá".

En este caso, según señala Xavier Guiteras Vila, investigador de mercados en Empírica Influentials & Research, la gran diferencia entre un frecuentista y un bayesiano "es que el primero desprecia toda información disponible previamente a la adquisición de los datos, sea aquella a nivel teórico o a nivel empírico; la estadística bayesiana, en cambio, no actúa en el vacío: el conocimiento previo se tiene en cuenta formal y explícitamente, e incorpora las probabilidades subjetivas, es decir, las que emergen de la propia intuición del investigador".

Estas probabilidades subjetivas no tienen por qué estar ancladas sólo en razones puramente intuitivas, sino tiene mucho que ver su pericia y experiencia previas.

De esta manera, la estadística bayesiana sí puede funcionar en un escenario donde la reducción del tamaño de la muestra necesaria para llevar a cabo un estudio de mercado, por ejemplo, no desvirtúe los resultados, ya que tiene en cuenta no solo datos previos generales, sino a cada momento los nuevos eventos que se van produciendo, así como expectativas de los propios investigadores acerca de cómo se comporta la realidad a la luz de su análisis estadístico.

La gran ventaja de la estadística bayesiana es que no opera aislada, pues se basa en conocimiento previo y proporciona un marco de análisis mucho más rico en tanto en cuanto deja mucha más libertad al investigador para que este pueda valorar hasta qué punto es probable que se produzcan determinados resultados en sus experimentos. Todo lo cual no deja de producir sarpullidos a los seguidores falsacionistas de Karl Popper.