Optimización: una visión teórica.

Los seres humanos estamos continuamente tomando decisiones a la hora de resolver problemas cotidianos, los cuales, normalmente, tienen diferentes tipos de restricciones que aumentan o disminuyen la complejidad del problema a resolver.

Estas decisiones van desde la selección de los calcetines que nos vamos a poner por la mañana para ir al trabajo, el momento en el que fijamos una reunión, o el coche que decidimos comprar.

Cada una de estas decisiones pueden depender de muchos aspectos interdependientes que, en algunos casos, entran en conflicto debido a las diferentes restricciones que tenemos que satisfacer para que la decisión sea válida.

La idea subyacente en la programación con restricciones consiste en la resolución de un problema sobre el que se han definido una serie de restricciones que deben cumplirse para poder obtener una solución de manera óptima, en el mejor de los casos, utilizando la menor cantidad de recursos.

Desde una perspectiva matemática podemos describir un problema de optimización cómo:

Un proceso de búsqueda de un valor o un conjunto de valores (variables), sobre los que se aplican un conjunto de restricciones, que permiten alcanzar el óptimo (máximo o mínimo absoluto) de una función objetivo. Aunque en algunos casos es suficiente encontrar un valor sub-óptimo que resuelve el problema.

Los primeros trabajos relacionados con la resolución de problemas con restricciones en el campo de la Inteligencia Artificial datan de los años 60, aunque los primeros experimentos ofrecieron resultados muy prometedores demostraron que este tipo de procesos necesitaba de grandes recursos computacionales y temporales para ofrecer resultados sub-óptimos.

Esta necesidad de minimizar los costes con el objetivo de poder ofrecer soluciones en un tiempo prudencial y con unos costes computacionales no muy elevados, dio lugar a la aparición de dos líneas de trabajo que intentaban resolver este tipo de problemas desde diferentes aproximaciones a nivel del proceso de búsqueda.

Por un lado, continuó el desarrollo de algoritmos que trataban de encontrar la solución óptima a un problema desde una perspectiva determinista, donde los algoritmos de búsqueda eran utilizados para generar una solución mediante la aplicación de operaciones de tipo determinista, dando lugar a los algoritmos de Constraint satisfaction problems (CSPs).

Mientras que, por otro lado, los investigadores comenzaron a desarrollar algoritmos de búsqueda que trataban de encontrar soluciones sub-óptimas en un tiempo muy pequeño aplicando operaciones no-deterministas o estocásticas donde los algoritmos de búsqueda eran utilizados para generar una solución mediante la aplicación de operaciones aleatorias o pseudo-aleatorias, dando lugar a los algoritmos genéticos.

Pero antes de explicar el funcionamiento de cada uno de estos algoritmos es importante definir dos conceptos: (1) el concepto de búsqueda y (2) el concepto de optimalidad.

El concepto de búsqueda

Los algoritmos de búsqueda son un tipo de algoritmo que permite buscar y/o generar soluciones (selección de valores) para un conjunto finito de variables.

Los algoritmos de búsqueda se basan en tres elementos básicos:

1. Un espacio, normalmente finito, de posibles estados que se corresponden con las posibles soluciones del problema sobre los que se realizará la búsqueda.
2. Un conjunto de acciones que nos permiten generar nuevos estados a partir de los estados generadores previamente.
3. Una función objetivo que permite definir la “calidad” de cada uno de los estados y/o soluciones que son generados de manera que el algoritmo pueda utilizar esta función para maximizar o minimizar el objetivo a la hora de guiar el proceso de búsqueda a la hora de seleccionar el siguiente nodo a expandir.

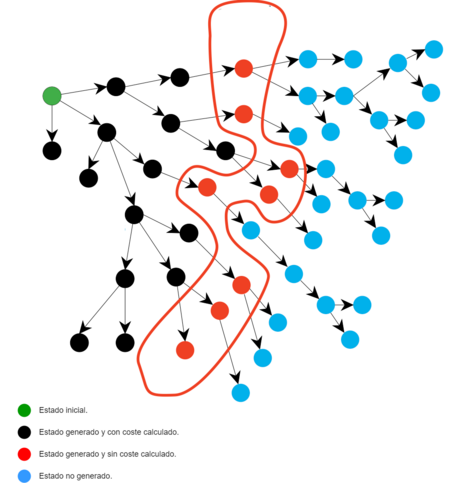
De forma que, desde la perspectiva de un proceso de optimización, el espacio de estados se corresponde con todas los posibles estados que existen en base a los rangos de posibles valores definidos para cada una de las variables que definen la solución; las acciones se corresponden con operaciones utilizadas por el algoritmo de búsqueda para generar nuevos estados que dan lugar a esas soluciones; y la función objetivo que permite guiar el proceso de búsqueda con el objetivo de maximizar o minimizar los valores obtenidos para cada solución.

El funcionamiento de los algoritmos de búsqueda pueden ser utilizados de diferente manera dependiendo de cómo se definan la estructura del espacio de estados y la estructura del espacio de acciones:

• La estructura del espacio de estados, o espacio de búsqueda, consiste en definir la manera de representar los estados que serán generados durante el proceso de búsqueda a la hora de encontrar una solución. Dependiendo del modelo de funcionamiento del algoritmo, los estados pueden representar soluciones válidas o inválidas del problema.
• La estructura del espacio de acciones consiste en definir las diferentes acciones que serán aplicadas para generar nuevos estados. Dependiendo de cómo sean definidas las acciones, los nuevos estados generados podrán corresponderse con soluciones inválidas del problema que tras la aplicación de una secuencia de acciones pueden dar lugar a una solución válida o soluciones válidas que resuelven el problema que con un grado de calidad muy baja.

Dependiendo de cómo el espacio de búsqueda es recorrido mediante la utilización de las acciones del espacio de acciones, tenemos diferentes modalidades de búsqueda:

• Búsqueda no informada o ciega es un modelo de búsqueda donde se realiza una búsqueda sobre el espacio de estados sin utilizar ningún tipo de información sobre el problema para encontrar una solución. Es decir, se aplica una estrategia de exploración del espacio de búsqueda exhaustiva que define como los estados son generados, siendo los algoritmos de búsqueda en amplitud (Breadth First Search, BFS, en sus siglas en inglés) o en profundidad (Deep First Search, DFS, en sus siglas en inglés) los algoritmos más conocidos de este modelo de búsqueda.
• Búsqueda informada o heurística es un modelo de búsqueda donde se realiza una búsqueda sobre el espacio de estados utilizando algún tipo de información del problema con el fin de minimizar el coste de encontrar una solución mediante la introducción de una función que guía el proceso de búsqueda. Esta función guía, denominada función heurística, permite calcular de forma estimada el coste que supone alcanzar el nodo meta permitiendo definir así el orden en que los estados del espacio de estados son seleccionados. Es decir, se aplica una estrategia de explotación de aquellas partes del espacio de búsqueda donde es posible que se encuentre la solución, siendo los algoritmos de Mejor Primero (Best First Search, BFS en sus siglas en inglés) y A* los más conocidos en este modelo de búsqueda.
• Búsqueda local es un modelo de búsqueda en el espacio de estados (soluciones) donde se utiliza una función de evaluación o fitness que nos permite evaluar la calidad de cada una de las soluciones generadas. Es decir, este tipo de algoritmos generan una solución inicial de forma aleatoria e intentan optimizarla mediante la aplicación de una serie de operaciones con el fin de mejorar la calidad de la solución con respecto a un conjunto de objetivos que tienen que ser maximizados o minimizados. Estas operaciones dan lugar a la generación de nuevas soluciones que espacialmente se encuentran muy próximas a las soluciones utilizadas para generarlas (las diferencias desde el punto de vista de la representación de la solución son muy pequeñas). Es decir, este tipo de algoritmos realizan una mezcla entre explotación y exploración con el objetivo de encontrar rápidamente una solución.

La principal diferencia entre las búsquedas informada y no informada y la búsqueda local es que las primeras van generando soluciones “inválidas” durante el proceso de búsqueda hasta encontrar una solución válida, y la segunda genera soluciones válidas de muy baja calidad durante todo el proceso de búsqueda hasta encontrar una que tenga una calidad mínima.

Es decir, los primeros algoritmos intentan encontrar la forma de generar la solución y el segundo intenta encontrar la solución sin hacer hincapié en cómo la solución ha sido generada.

El concepto de optimalidad

Un proceso de optimización, normalmente, consiste en buscar la mejor solución posible de entre todas las posibles soluciones que existen para resolver un problema.

A la hora de identificar si una solución es o no óptima es necesario definir lo que se conoce como concepto de optimalidad que permite indicar de manera completa e inequívoca si una solución es o no óptima con respecto a todas las demás soluciones que existen en base a un determinado concepto.

Para conseguir determinar si una solución es óptima se suelen aplicar comúnmente dos técnicas, aunque existen otras:

• Generar y comprobar todas las soluciones que existen con el objetivo de identificar cuáles de ellas son las soluciones óptimas.
• Definir una función matemática que permita demostrar desde una perspectiva matemática que una solución es óptima.

La mayoría de las técnicas actuales que intentan encontrar una solución óptima, como los CSP, suelen basarse en el primer concepto para asegurar que han encontrado una solución óptima tras expandir de manera completa o casi completa el espacio de búsqueda pudiendo comparar las diferentes soluciones para identificar aquella que es óptima.

Por ese motivo se suelen aplicar técnicas que son capaces de encontrar soluciones sub-óptimas cómo los algoritmos genéticos.

Constraint satisfaction problems (CSP)

Los Constraint Satisfaction Problems (CSPs) son un tipo de técnica de resolución de problemas con restricciones que utilizan algoritmos de búsqueda informada para la generación de una solución.

Para resolver un problema de este tipo mediante un CSP es necesario modelar el problema de manera específica de la siguiente manera:

• Un conjunto finito de variables que describe las posibles soluciones representadas como una secuencia de variables (V = {v1, v2, v3,....., vn}).
• Un conjunto finito de valores, denominados dominios, que definen los posibles valores que pueden ser asignados a las variables y representados de la siguiente forma (D = {d1, d2, d3,....., dn}). Estos dominios pueden ser de tipo discreto o de tipo continuo.
• Un conjunto finito de restricciones representados como una secuencia de restricciones (R = {r1, r2, r3,......, rn}).

Para la resolución de este tipo de problemas se aplican tres tipos de técnicas: (1) Búsqueda, (2) técnicas inferenciales y (3) técnicas híbridas; siendo la búsqueda una de las técnicas más comunes para la resolución de este tipo de problemas.

Búsqueda mediante generación y comprobación

Este método de búsqueda no informada consiste en generar todas las posibles combinaciones de variables (soluciones) de forma sistemática y comprobar, de manera secuencial para cada solución, si cumple con las restricciones definidas en el problema.

En caso de que se encuentre una solución válida se podrá finalizar el proceso de búsqueda o continuar hasta encontrar la solución óptima, lo que supondrá la expansión completa del espacio de búsqueda.

Por ejemplo, si quisiéramos resolver el famoso problema de las 8-Reinas se podría modelizar mediante un CSP utilizando 84 restricciones y 88 = 16. 777.216 posibles de asignaciones de variables (soluciones), de manera que el espacio de búsqueda estaría formado por más 16 millones de soluciones sobre las que buscar una solución óptima.

Búsqueda mediante Backtracking

Este método de búsqueda no informada utiliza un algoritmo de búsqueda en profundidad donde las operaciones consisten en ir añadiendo variables siempre y cuando todas las variables anteriores añadidas sean consistentes sobre las restricciones.

Es decir, dado el estado inicial, donde no hay ninguna variable asignada, se asigna un valor a una variable y se comprueba si es consistente en base a las restricciones definidas para el problema. Si es consiste se realiza una asignación sobre otra variable comprobando si sigue siendo consiste; si es así, se siguen asignando valores a las variables hasta que se encuentre una solución que cumpla con todas las restricciones.

Al igual que en el algoritmo anterior, el sistema podrá encontrar la solución óptima si se realiza una expansión completa del espacio de búsqueda “válido”, ya que en este caso las soluciones inválidas son podadas.

Algoritmos genéticos

Los algoritmos genéticos son un tipo de técnica de resolución de problemas con restricciones que utilizan algoritmos de búsqueda local estocástica basados en la teoría de la evolución de Charles Darwin, quien describió que el proceso de evolución de las especies se basa en un proceso competitivo donde los individuos más aptos son aquellos que sobreviven transfiriendo su material genético a sus descendientes.

Esta idea se puede extrapolar para construir un algoritmo de búsqueda sobre un espacio de búsqueda que está formado por todos las posibles soluciones del problema, donde las mejores soluciones al problema que van siendo generadas o “encontradas” son las que sobreviven, ya que se han adaptado de la mejor manera al entorno.

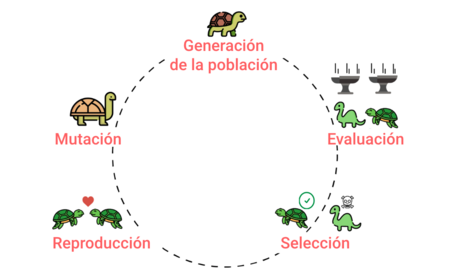
Los algoritmos genéticos comienzan su funcionamiento mediante la creación de una población inicial de soluciones (individuos) mediante la utilización de valores predeterminados y/o aleatorios para cada uno de los cuales se calculará un valor numérico denominado fitness (evaluación) que nos permitirá definir de manera numérica el grado de adaptación de la solución.

A continuación, comienza el proceso de búsqueda, que consistirá en una serie de iteraciones donde se ejecutarán una serie de procesos que permitirán generar una nueva población que puede que mejore el grado de adaptación de las soluciones.

En cada una de las iteraciones se ejecutará al menos las operaciones de evaluación, selección, reproducción, mutación dando lugar a una nueva población de soluciones que tal vez tenga una mejor adaptación al problema que queremos resolver.

Fase de evaluación

La fase de evaluación es una de las más importantes del proceso evolutivo, ya que permite calcular para cada una de los individuos de la población su grado de “calidad” mediante la utilización de la función de fitness. Este proceso permitirá identificar a aquellos individuos (soluciones) que serán utilizados para la generación de la población siguiente.

Fase de selección

La fase de selección es una fase opcional que no siempre ocurre y que permite seleccionar un subconjunto de individuos (soluciones) de la población actual en base a su grado de calidad. Este proceso permite eliminar individuos de baja calidad con el objetivo de generar una población de mayor calidad en la siguiente iteración.

En algunos casos, esta fase no se ejecuta y se utilizan todos los individuos de la población actual para generar la siguiente con el objetivo de no eliminar información “genética” que podría ser útil.

Fase de reproducción

La fase de reproducción consiste en el proceso de combinación de los individuos (soluciones) disponibles, independientemente de si se ha aplicado la fase de selección o no, para generar los nuevos individuos de la siguiente población mediante la combinación de diferentes fragmentos de los individuos seleccionados.

Es decir, cada individuo se divide en diferentes pedazos y estos se combinan con los de otros individuos con el objetivo de generar un individuo (solución) con una estructura válida, siendo los dos modelos de reproducción más utilizados los siguientes:

• Reproducción simple donde se seleccionan dos individuos que son divididos en dos pedazos mediante un punto de corte que son utilizados para generar dos nuevos individuos, como se presenta en la siguiente imagen, como resultado de la reproducción.

• Reproducción múltiple donde dos individuos se dividen en n pedazos mediante n-1 puntos de corte que son distribuidos de manera uniforme entre los dos nuevos individuos resultado de la reproducción.

Fase de mutación

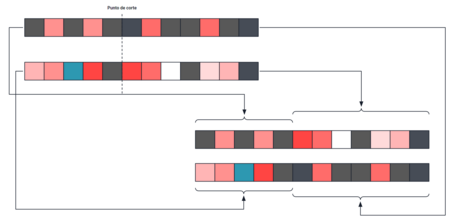
La fase de mutación consiste en aplicar cambios de tipo aleatorio sobre los nuevos individuos generados durante la fase de reproducción con el objetivo de generar mejores individuos (soluciones) mediante la introducción de valores que puede que actualmente no se encuentren en la solución.

Conclusiones

Las diferentes técnicas de optimización disponibles nos permiten resolver problemas muy complejos del mundo real con diferente grado de exactitud y complejidad.

Por un lado, podemos intentar encontrar una solución óptima al problema mediante la utilización de técnicas deterministas que expanden casi en su totalidad el espacio de búsqueda con el objetivo de asegurar esa solución óptima a coste de un gran número de recursos computacionales y temporales.

Por otro lado, podemos intentar encontrar una solución sub-óptima utilizando cualquiera de las técnicas disponibles, disminuyendo en gran medida los recursos computacionales y temporales necesarios para su “generación” consiguiendo así resultados que pueden ser aceptables desde la perspectiva del problema.

Como conclusión, podemos indicar que las diferentes técnicas de optimización que existen actualmente nos permite obtener soluciones a problemas de un nivel de complejidad elevado de manera sencilla.