Estadísticas bayesianas y estadísticas frecuentistas: herramientas para el ahorro de las empresas.

La idea fundamental del Teorema de Bayes, según muestra Enrique Moral-Benito, doctor por el Centro de Estudios Monetarios y Financieros (CEMFI) y económetra, es que puedo modificar mis creencias una vez que observo los datos en tiempo real. "Un ejemplo sería el juego de ruleta en el que hay 38 posibles huecos en los que la bola puede acabar con la misma probabilidad (desde el 1 hasta el 36 más el 0 y el 00 en la americana).

Si un jugador apuesta al número 7, yo pienso que la probabilidad de que gane es 1/38 (aproximadamente 2,63%). Esta es mi creencia a priori, antes de anotar ningún dato. Ahora imaginemos que consigo mirar cuando la bola ha parado y aunque no puedo leer el número en el que ha caído, puedo ver que el hueco es de color rojo.

Ello puede interpretarse como los datos que observo, la muestra que tengo disponible. Pues bien, dado que hay 18 huecos rojos en la ruleta y el número 7 es uno de ellos, actualizo mis creencias y ahora pienso que la probabilidad de que gane es 1/18 (5,55%). Modifico mis creencias sobre la probabilidad de ganar (o parámetro de interés)"

Sabemos que si tenemos una muestra suficientemente grande (aquí, como siempre, no está claro qué es una muestra suficientemente grande porque dependerá de la complejidad del problema analizado, del presupuesto disponible, del plazo de entrega...) la creencia a priori del investigador se ve dominada por los datos, y su influencia en el resultado final disminuye hasta hacerse inocua con una muestra de infinitas observaciones.

Sin embargo, los contrastes de hipótesis parecen más naturales en el marco bayesiano. Para un bayesiano convencido, un p-valor o un t-ratio es una herejía, ya que lo único que necesitamos para contrastar hipótesis es tener la distribución a posteriori de los parámetros, como explicará en Big Data Spain con su ponencia Roland Vollgraf, del departamento de Inteligencia de Datos de Zalando.

De todas maneras, solo una salvedad: teniendo en cuenta la conexión entre ambos enfoques estadísticos en la práctica matemática y ante la posibilidad de obtener los mismos resultados bajo ambos métodos, los bayesianos argumentarían que su interpretación del problema es siempre más intuitiva y natural.

Recordemos que un bayesiano proporcionaría conclusiones del tipo: "hay un 95% de probabilidad de que el parámetro esté entre 2,6 y 5,5”; sin embargo, un frecuentista afirmaría: “si generáramos 100 muestras aleatorias del mismo tamaño y repitiéramos la estimación 100 veces, aproximadamente en 95 de ellas el parámetro estimado estaría entre 2,6 y 5,5”. Cuestión de enunciado.

Por resumir, en el enfoque bayesiano se combinan evidencias subjetivamente acumuladas con la información objetiva de los datos. Para Juan Tomás Bradanovic, pensador y analista chileno, la mejor descripción es ésta: "la diferencia esencial entre el pensamiento clásico y el bayesiano radica en que el clásico se pronuncia probabilísticamente sobre los datos a partir de supuestos; en tanto que el bayesiano se pronuncia (también probabilísticamente) sobre los supuestos partiendo de los datos".

Por eso la probabilidad bayesiana se llama probabilidad subjetiva o condicional: contiene información sobre observaciones y experiencias previas a diferencia de la probabilidad frecuentista, que se basa solo en el análisis de las frecuencias de los datos y no admite suposiciones a priori de ninguna clase aparte de las hipótesis.

Esto no deja de crear cierta polémica sobre "lo científico" de las pruebas, pero en el caso de los frecuentistas o parametrista, también muchas veces basan sus resultados partiendo de aquello que "está estadísticamente comprobado". Lo que nos lleva a un imaginario diálogo en donde Mulder (el bayesiano) le diría a Scully (la frecuentista): "la Verdad está ahí afuera, pero los humanos tenemos problemas para evaluarla (y el Gobierno negará todo conocimiento)".

El enfoque bayesiano no sustituye el estudio de las frecuencias, lo enriquece con experiencias anteriores ya que puede ir refinando hacia atrás los resultados obtenidos en cada iteración.

Un ejemplo extremo es que si en los últimos 4.500 millones de años en Cuenca ha salido el sol por el levante, suponemos que la probabilidad de que mañana vaya a volver a salir el sol es más alta con un estudio bayesiano de lo que sería con un análisis de estadística clásica, que no da ningún peso a la historia pasada.

Pero cuando un médico pronostica "le quedan unos seis meses de vida", querríamos creer que el galeno nos está facilitando esta información no sólo en base a un análisis de las frecuencias para esta dolencia, sino que además incorpora su experiencia de otros diagnósticos similares, y en especial nuestro propio historial clínico. "Las conclusiones son afectadas por la premisa, pero si ésta es bien formulada, más que un defecto sería una ventaja", señala Juan Tomás Bradanovic.

Esta aparente contradicción entre el análisis inicial y el basado en la verosimilitud, para Eduardo Gutiérrez Peña, profesor de Estadística en la Universidad Nacional Autónoma de México (UNAM) se debe en gran parte a que, en general, nuestra intuición no es suficientemente buena al procesar evidencia probabilística.

"La prevalencia puede pensarse como la probabilidad a priori (o inicial) que describe nuestros juicios sobre el evento, antes de conocer el resultado de la prueba. Pero al observar un resultado, nuestros juicios cambian y la probabilidad del evento se modifica a posteriori (o final), pues describe nuestra opinión sobre la ocurrencia del evento".

El Año Internacional de la Estadística

Hace dos años se celebró el Año Internacional de la Estadística (#Statistics2013). Y, ¿qué es la estadística? La ciencia que estudia los fenómenos aleatorios; es decir, aquellos que no se pueden predecir con certeza. Y ¿cómo se muestra normalmente? Con una curva del tipo campana de Gauss (en la clásica) y con una trompeta o de cualquier otro modo en la bayesiana.

En la opinión de Enrique Moral-Benito, del CEMFI, en general ninguno de los dos enfoques es mejor que el otro. "Cada uno tiene ventajas y desventajas. La visión frecuentista domina actualmente la práctica econométrica, pero es también cierto que está creciendo el interés en lo bayesiano, en buena medida debido al desarrollo de la capacidad computacional de los ordenadores".

En la actualidad, el uso del Teorema de Bayes en pruebas de diagnóstico médico es bastante común. En cambio, es mucho más controvertido su uso en análisis estadísticos generales. Una de las principales críticas al enfoque bayesiano es que dos personas cuyas opiniones iniciales difieren podrían llegar a conclusiones distintas a pesar de observar exactamente los mismos datos (Mulder y Scully de nuevo).

De esta forma, mientras los métodos estadísticos tradicionales se preguntan qué nos dicen los datos acerca del valor del parámetro (ignorando con ello toda evidencia externa a los datos), los métodos bayesianos se preguntan explícitamente cómo cambia nuestro estado de información acerca del valor del parámetro (o de cualquier otra cantidad de interés) a la luz de los datos observados.

Si bien esto es cierto, conforme se va acumulando la evidencia, las opiniones de esas dos personas deberían converger. En este sentido, la objetividad a la que aspira la ciencia podría replantearse de manera más realista como un "consenso de subjetividades".

Al admitir información adicional, los métodos bayesianos reconocen que cada problema es distinto y promueven que el procedimiento de análisis se adapte al problema en cuestión, y no al revés; como consecuencia, tienden a ser más flexibles. Sin embargo, para poder hacer esto posible, la implementación de las técnicas bayesianas usualmente requiere de un esfuerzo computacional muy alto.

La mayor parte de este esfuerzo se concentra en el cálculo de ciertas características de la distribución final del parámetro de interés. Por ejemplo, hay que integrar para pasar de una distribución conjunta a una colección de distribuciones marginales que sean útiles para hacer inferencias sobre los parámetros de interés.

En la gran mayoría de los problemas las integrales requeridas no pueden resolverse analíticamente, por lo que es necesario contar con métodos numéricos eficientes que permitan calcular o aproximar integrales en varias dimensiones.

Afortunadamente, durante la segunda mitad del siglo XX se comenzaron a desarrollar técnicas numéricas flexibles y eficientes basadas en métodos de simulación estocástica.

Esto, aunado al desarrollo de la tecnología que ha dado lugar a una mayor capacidad de procesamiento y de almacenamiento de los equipos de cómputo gracias a la virtualización, el Cloud Computing y el Big Data, está provocando un auge de los métodos bayesianos.

Concluyendo

La discusión científica y filosófica sobre el uso del Teorema de Bayes para hacer inferencia estadística ha durado más de un siglo y se ha centrado en aspectos fundamentales del quehacer científico: cómo analizamos la evidencia, cómo cambia nuestra opinión conforme recibimos más información, o cómo tomamos decisiones en presencia de incertidumbre.

Por concluir, las siguientes propiedades caracterizarían al enfoque bayesiano de la estadística:

• Uso de información adicional: cada problema es único y tiene su propio contexto, del cual se deriva la información inicial (o cualquier otra característica) sobre el parámetro de interés.
• Interpretación subjetiva de probabilidad: depende del estado "informacional" del individuo que las asigna, por lo que en ningún momento pretende ser un enfoque puramente “objetivo”.
• Coherencia interna: al considerar el valor del parámetro como aleatorio, se desarrolla de manera natural y por lo tanto no presenta contradicciones internas.

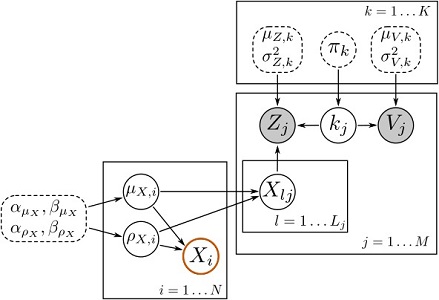
Sin destripar lo que Roland Vollgraf, el experto en análisis científico de datos en Zalando, nos va a contar en #BDS15, el próximo día 15 de octubre, avanzar que "desarrollar nuestro nuevo modelo de medición y verificar que funcionara tomó un poco de esfuerzo.

Pero valió la pena, porque ahora tenemos estimaciones automáticas del peso para cada artículo de Zalando, lo que ahorra tiempo a los manipuladores; y además, una manera fiable de saber la precisión de nuestras estimaciones.

Pero lo más importante: nuestros trabajadores del almacén pueden ahora centrarse en conseguir que tu moda llegue lo más rápidamente posible a tu casa. Eso no es sólo ahorrar dinero, eso no tiene precio".